Brian Greene’s The Elegant Universe is my favorite non-fiction read. I’ve traveled its pages only three times thus far, because its concepts give my brain a workout. The prose is elegant (like our universe!) and accessible, but understanding the physical underpinnings of the cosmos is not something I do easily. I labor. And, yet, by book’s end, I feel like I’ve been peeking over the shoulder of the divine, granted a view of miracle. That’s worth some effort!
Greene starts with an entertaining overview of Einstein’s principles of special relativity and general relativity. I grin through this section, because his examples are amusing. In my latest perusal, I noticed a nugget about how we navigate spacetime that had previously escaped either my notice or my memory. (Amidst all the other wonders presented.)
Time Travel
We are always in motion, even when sitting still, both because we traverse time and because our planet whooshes ever onward around our sun, around our galaxy, and across the universe. However, Einstein’s principles of relativity allow me to declare myself as still in space when occupying my armchair reading The Elegant Universe.
When I’m not sitting and reading (or sitting and writing!), I’m moving through both space and time. Compared with the speed of light – 670 million mph – I’m traversing space very slowly, at 1 or 2 mph when I’m strolling in the garden, 25 mph driving down a residential street, or 300 mph jetting through the sky. But guess what? I’m traveling through the dimension of time very fast. At the speed of light, in fact! Of course, so is everything and everyone around me. So I don’t notice my speed!
Wow! I’d like to see Greene explore the ramifications more thoroughly, but he’s a man on a mission with a lot of conceptual ground to cover. His purpose is not to dance in Einstein’s preserve, but to connect superstring theory to it. He continues through the history of physics and into the paradox arising between the rules governing the macrocosm and those governing the microcosm. When physicists want to understand black holes or the moment of the big bang, they cannot, because these conditions require both general relativity and quantum mechanics. Which do not mix! Superstring theory proposes a solution for the paradox.
Superstrings Calm the Quantum Foam
When we think about the smallest particles that make up the physical universe – electrons and quarks – we consider them to be points that have no height or width or depth. They are dimensionless.
This way of thinking causes problems.
It means we must deal with quantum tunneling. At a sufficiently small size, many of the usual rules of the universe no longer pertain. Gravity? Nope. Cause and effect? Gone. Knowing where and when? Farewell certainty.
Envisioning the smallest particles as strings rather than dimensionless points solves these problems in two ways.
First, the strings of superstring theory have length. They are loops of about the Planck length. “What is the Planck length?” you ask. It is very small: a millionth of a billionth of a billionth of a billionth of a centimeter. Greene gives us an analogy: if one atom were the size of the entire known universe, the Planck length would be the height of an average tree!
Very small, indeed, but NOT zero. Which means that we cannot probe physical reality below a certain size. Below the Planck length, in fact. Because nothing is smaller than that. In a sense it doesn’t exist.
And the quantum foam, where the rules of the universe go awry, exists mathematically only at scales smaller than the Planck length. But if we know the fundamental blocks of matter – strings – are too big to fit into the mathematical quantum foam, then all matter remains within a spacetime where the usual rules apply.
That is one way of looking at the issue. Superstring theory also gives us a second way.
In the Grandstands for an Event
Consider two particles traveling at high speed that collide, say an electron and a positron (an electron’s antimatter counterpart).
The particles collide and are annihilated, releasing energy as a photon. The photon travels some while and then releases it energy, transforming into two particles that go their separate ways.
A physicist’s diagram of the event would like like this.
And here’s the difficulty: Einstein’s relativity principles state that different observers would not agree about exactly when and where the two particles collided. When considering point particles, that truth seems impossible.
Which is it?
This?
Or this?
How can it be both?
Now consider how it looks if the particles are strings.
One person might see the collision like this, at a certain time and place.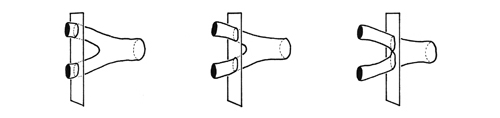
While another might see it like this, at a different time and place.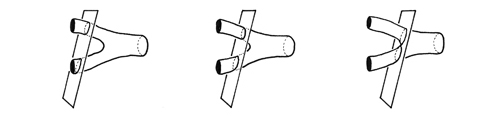
No paradox at all. The quantum foam (which is paradox) has smoothed out.
Greene goes on to discuss the further wonders of superstring theory: Calabi-Yau spaces and their transformations, M-theory, and the striking similarity between black holes and strings. It’s an incredible romp through the foundations of physical reality. Greene leaps from marvel to marvel, ending with the tantalizing possibility that superstring theory might allow us humans to graze the ultimate why.
I’ll be re-reading The Elegant Universe every few years . . . when my brain is ready to stretch and work!
The Elegant Universe at Amazon
The Elegant Universe as an ebook at Kobo
For more cool science trivia, see:
Sol
Water
Anatomy of a Pitch
